Motor electromotive force calculation

气隙磁密波形系数

$K_f=\frac{B_{\delta1}}{B_ \delta}=\frac{4}{\pi}\sin\frac{\alpha_i\pi}{2}$

空载反电势是由电枢绕组切割空载气隙基波而产生的

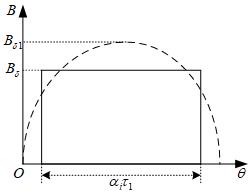
永磁体产生的每极气隙磁通

$\phi_{\delta0}=B_{\delta m}\alpha_i\tau_1L_{ef}=B_{\delta av}\tau_1L_{ef}$

采用静态场求磁密曲线再求$B_{av}$

空载反电势

$E_0=4.44fNK_{dp}\phi_{\delta0}K_\phi$

永磁体产生的每极基波磁通

$\phi_0=\frac{2}{\pi}B_\delta\tau_1L_{ef}$

采用静态场FFT求气隙磁密基波幅值$B_\delta$

空载反电势

$E_0=4.44fNK_{dp}\phi_0$

气隙波形系数

$K_\phi=\frac{\phi_0}{\phi_{\delta0}}=\frac{8}{\alpha_i\pi^2}\sin\frac{\alpha_i\pi}{2}$

To be continued.🧀